3D and 4D Cartesian Graphs

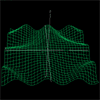
These graphs are visualizations of functions where Z = f(X,Y) (produces a still 3D surface) or Z = f(X,Y,Time) (produces a moving 3D surface)

All of these are rotatable using the mouse, click to start/stop time. Coming soon is a user-definable function grapher.

The 4D function Z = sin(X*Y/10 + t)

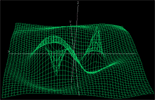A 4D function resembling the interactions between two sources of waves in a liquid.

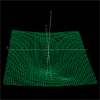A 4D function resembling Einstein's concept of gravity as warping spacetime. Here, the sun is the central dip, and the earth is the smaller dip which is orbiting the sun.

I have several projects in mind which build on this kind of programming:

    A physical realization of a 4D function; an actual moving 3D surface. This could be achieved by controlling a squarely arranged array of motors which each drive something up and down according to the function Z values at the given (X,Y) of the particular motor. Then if you put some kind of "skin" on the whole assembly, you would have a real moving 3D surface. I realize this kind of project has no real purpose except for the learning experience, but I believe it may be of interest to the art world.

    Have the program rotate a curve about a given line. Then this program could be used to visualize calculus problems involving such rotation, and may be useful for high school calculus teachers.

    Instead of defining each Z by a function, have all Z points dependent on surrounding points. So when one point is moved, that movement moves other points, which move other points etc. This may be used in the future to model actual physical things, like water or cloth.